In class, we have been looking at binary search trees, and how they can be used to efficiently perform certain actions. We have also learned that some operations, such as finding whether or not a certain binary search tree contains a value or not, have a time complexity proportional to their height, and therefore keeping the height of a tree to a minimum is desirable.
Specifically, in a lab, we were told to find a way to insert a list of values into a BST while keeping the height of such small. Although we were advised to use a random selection in order to achieve this, I was convinced something more efficient was possible. It turns out I was right. By pre-sorting the list of values to be inserted into the binary search tree, it is possible to construct a recursive algorithm that inserts each element in a specific order as to obtain a balanced search tree. Consider the following:
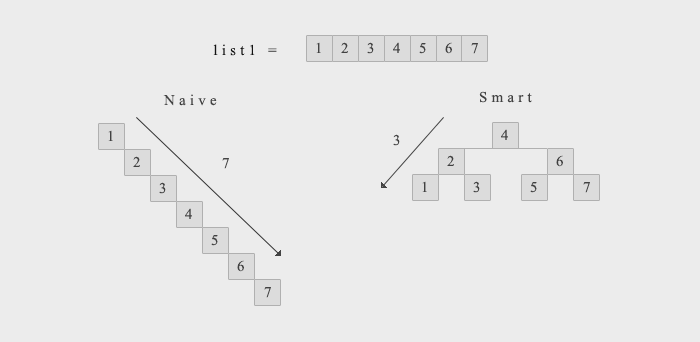
Since the list is sorted in a non-decreasing order, it definitely doesn’t make sense to insert the elements in the order they are. This is because the naive tree would be produced. Alternatively, we could shuffle randomly the tree (which I believe is what the course instructors wanted us to do in the assignment). However, we can do better. In fact, we can get the smart tree every time.The code I came up with in order to guarantee this is the following:
class BST:
# ... other methods here
def insert(self, data):
"""Insert data, if necessary, into this tree.
Precondition: if data is a list, it is pre-sorted in
non-decreasing order.
"""
# Insert list
if(isinstance(data, list)):
midata = len(data) // 2
self.insert(data[midata])
if(len(data) > 1):
self.insert(data[:midata])
if(len(data) > 2):
self.insert(data[midata + 1:])
else:
self._root = _insert(self._root, data)
Here, _insert(...) is a function that adds the value data to self in the correct position. What’s important is that, by choosing the middle element of each array and sub-array it is possible to form a balanced and efficient binary search tree. It is important to note that the list being inserted should be sorted, otherwise the method would not produce a particularly efficient binary tree.
If you are interested in seeing the entire code (including the function _insert, and the other methods of BST), you can download my solution to the entire assignment here!